Introduction

Conventional wheel suspension system relies on the upward freedom of wheels relative to the load carried by wheels to overcome obstacles and reduce shock on the load. It uses strong weight bearing spring or equivalence to support the load on wheels. In one extreme application, the in-line roller skate, applying the conventional suspension system will inevitably increase the gravity center of the skater because of the upward freedom of the wheels. Can we have a wheel suspension mechanism which can keep the gravity center of the load as low as if no suspension system were used, which uses none or little spring (or equivalence) and thus introduces no vibrations commonly associated with them, and which is efficient even for relatively large obstacles ? Here we study a non conventional wheel suspension mechanism which seems to give positive answers to the above questions.
 
  Since the invention of the wheel, the fundamental mechanism of wheel suspension system has not changed. Whether it is in the form of spring sheet, trailing arm, leading arm or telescope suspension, they all are based on the same idea that when the wheel encounters an obstacle, we want the wheel instead of the load which the wheel is carrying to bounce up. Therefore allowing upward freedom of the wheel seems to be inevitable for a wheel suspension system. Here we introduce a suspension mechanism which seems to be just the opposite of the conventional mechanism. It could function in some situations where the conventional suspension mechanism fails and could even outperform the conventional suspension system in low speed. The new suspension mechanism complements the existing suspension mechanism and could have broad applications. We will try to explain the conceptual ideas here without going into the details of the physical and mathematical modeling of more complicated variations.
 
  The concept of tangential suspension mechanism can be easily described by use of a bicycle front wheel. First we look at a bicycle front wheel with no suspension system hitting a bump on the road as in Fig. 1.

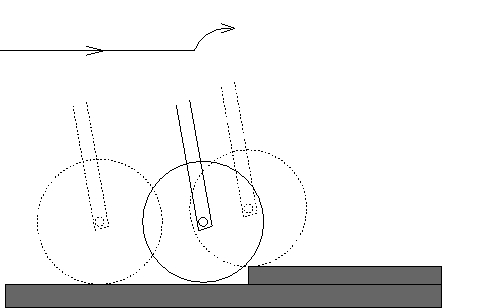
The curve above the bicycle illustrates the trajectory of the gravity center of the frame. A sharp corner in the curve indicates that there is a Dirac delta function in the second derivative of the curve, which corresponds to the shock the rider feels.
 
  Now let's use a pair of swing arms hanging vertically with one ends attached to the wheel axle, with the other ends connected pivotally to the bicycle front forks at a position right below the wheel center. Assume that the mass of the wheel is negligible comparing to the mass the whole bicycle. When the wheel encounters an obstacle, unlike conventional suspension system in which the wheel will bounce up, the wheel will first stop because the swing arm is perpendicular to the ground and has essentially no forward component of force acting on the wheel. Then the swing arm starts to swing around the wheel center forward and upward.

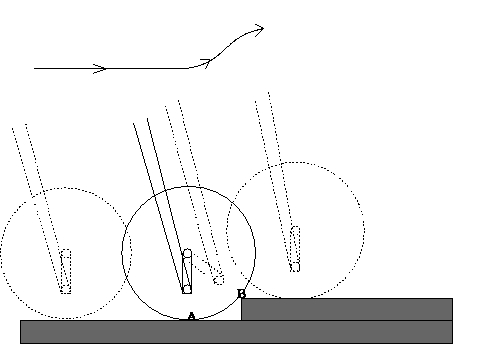
When the swing arm swings pass a critical angle (i.e., the angle between the line segment connecting the wheel center and the ground contact point "A" and the line segment connecting the wheel center and the obstacle contact point "B"), the net force acting on the wheel will break the equilibrium of the wheel and drive the wheel to roll over the obstacle. The resulting trajectory of the mass center of the frame (see the curve in Fig. 2) will be a continuously differentiable curve (made of tangentially connected smooth segments) during this time period, so that there is no shock force acting on the frame.
 
  Note that in the simple suspension setting of Fig. 2 there is no need to use any form of weight bearing spring! Besides that, the wheel with tangential suspension is able to overcome large obstacles at low speed without generating shock yet still keep the gravity center of the frame as low as if no suspension were used. Its simplicity could find it applications in almost all the low speed transportation equipments in the industry and everyday life, such as wheel chair, roller skate, scooter, wheel dolly, baby stroller, wheel carts, bicycle, trailer etc.

Compensation of the Rolling Resistance

Under construction.